Pythagorean Tuning in the Key of E

Pythagorean Tuning is accomplished by bringing a series of third harmonics into the same "octave" range. The third harmonic is 3 times the fundamental frequency, and the range of an "octave" is from the fundamental to the second harmonic, which is at twice the frequency of the fundamental.
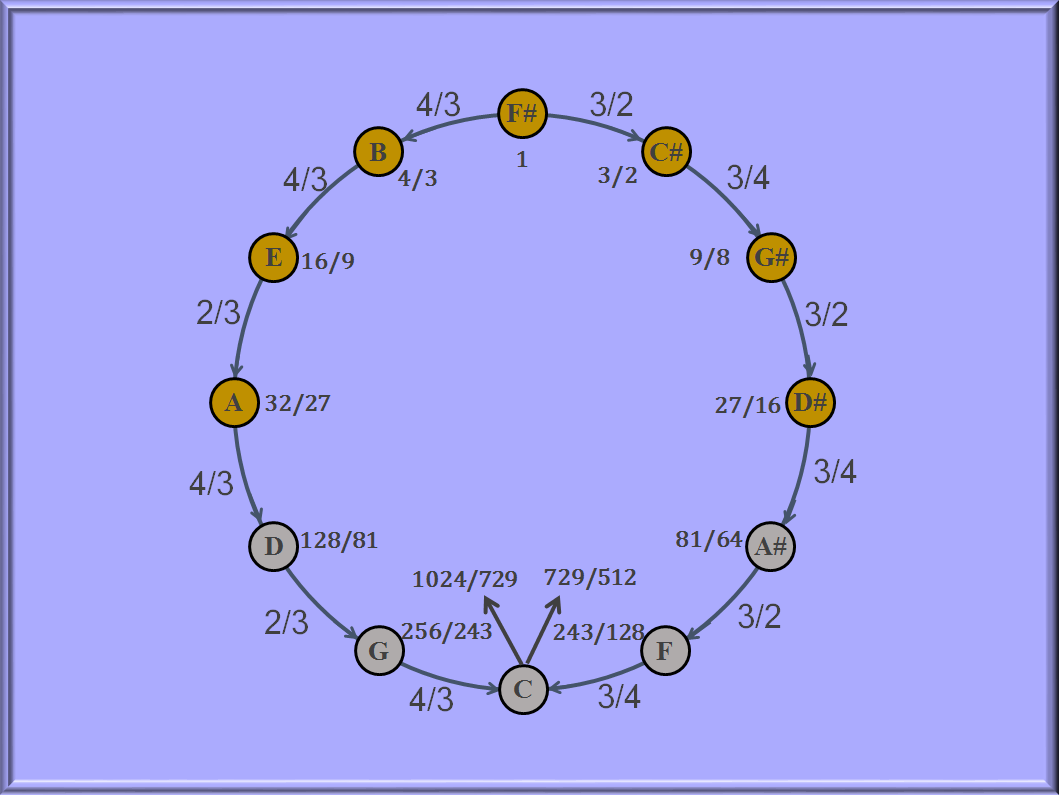
Pythagorean tuning in the "Key of E" can be accomplished by starting on a fundamental "C" and setting "G" to a frequency that is 3/2 of the original "C". "G" is the third harmonic of "C" reduced by one "octave" (divided by 2). Next, "D" is generated as the note that is 3/4 the frequency of "G" - the third harmonic of "G" divided by 4 to bring it into the same "octave" range.
The process of multiplying by 3 and dividing by 2 or 4 as necessary continues until twelve notes have been generated. The frequency of the twelfth note so generated ("C", but sometimes called "C-Flat" in this context) is very close to the frequency of the original "C". The interval between these two "C" notes, approximately 1/8 of a whole tone, is called the "Pythagorean Comma" or the "Ditonic Comma":
1024/729 = 1.404664
729/512 = 1.423828
1.423828/1.404664 = 1.013643 = (729)(729)/(1024)(512) = (3^12)/(2^19) = 531441/524288
The scale can as readily be constructed by beginning with the F#, which is how it is depicted in the figure. Proceed by multiples of three (and divisions by factors of 2) for six notes until the "C" is reached. Next, proceed by multiples of two with divisions by three for six notes in the opposite direction, meeting up on "C". One of the two "C" notes is chosen in order to retain a 12-note scale.
When the scale is viewed as a series of intervals based on the third harmonic, F# is seen to be at the center of the "Key of E". Although the 7 notes in the "Key of E" are the most frequently heard, all twelve notes of the scale are used in Moonlight Sonata and Dark Moon. The notes might sound more dissonant the farther they get from the F#.
A portion of the actual scale that was used in Dark Moon is shown below:
| Pythagorean-Tuned Notes Relative to Reference A=440 | |||||
| Note | Integer Ratio | Decimal Ratio | Frequency | Cents off of EQT | Half-Step Interval |
| C | 32/27 | 1.185 | 130.370 | -5.85 | 1.068 |
| C# | 81/64 | 1.266 | 139.219 | 7.84 | 1.053 |
| D | 4/3 | 1.333 | 146.667 | -1.95 | 1.053 |
| D# | 1024/729 | 1.405 | 154.513 | -11.69 | 1.068 |
| E | 3/2 | 1.500 | 165.000 | 1.96 | 1.053 |
| F | 128/81 | 1.580 | 173.827 | -7.80 | 1.068 |
| F# | 27/16 | 1.688 | 185.625 | 5.87 | 1.053 |
| G | 16/9 | 1.778 | 195.556 | -3.90 | 1.053 |
| G# | 4096/2187 | 1.873 | 206.017 | -13.63 | 1.068 |
| A | 1 | 1.000 | 220.000 | 0.00 | 1.053 |
| A# | 256/243 | 1.053 | 231.770 | -9.74 | 1.068 |
| B | 9/8 | 1.125 | 247.500 | 3.91 | 1.053 |
| Middle C | 32/27 | 1.185 | 260.741 | -5.85 | 1.068 |
| C# | 81/64 | 1.266 | 278.438 | 7.84 | 1.053 |
| D | 4/3 | 1.333 | 293.333 | -1.95 | 1.053 |
| D# | 1024/729 | 1.405 | 309.026 | -11.69 | 1.068 |
| E | 3/2 | 1.500 | 330.000 | 1.96 | 1.053 |
| F | 128/81 | 1.580 | 347.654 | -7.80 | 1.068 |
| F# | 27/16 | 1.688 | 371.250 | 5.87 | 1.053 |
| G | 16/9 | 1.778 | 391.111 | -3.90 | 1.053 |
| G# | 4096/2187 | 1.873 | 412.035 | -13.63 | 1.068 |
| A | 1 | 1.000 | 440.000 | 0.00 | 1.053 |
| A# | 256/243 | 1.053 | 463.539 | -9.74 | 1.068 |
| B | 9/8 | 1.125 | 495.000 | 3.91 | 1.053 |
| C | 32/27 | 1.185 | 521.481 | -5.85 | 1.068 |
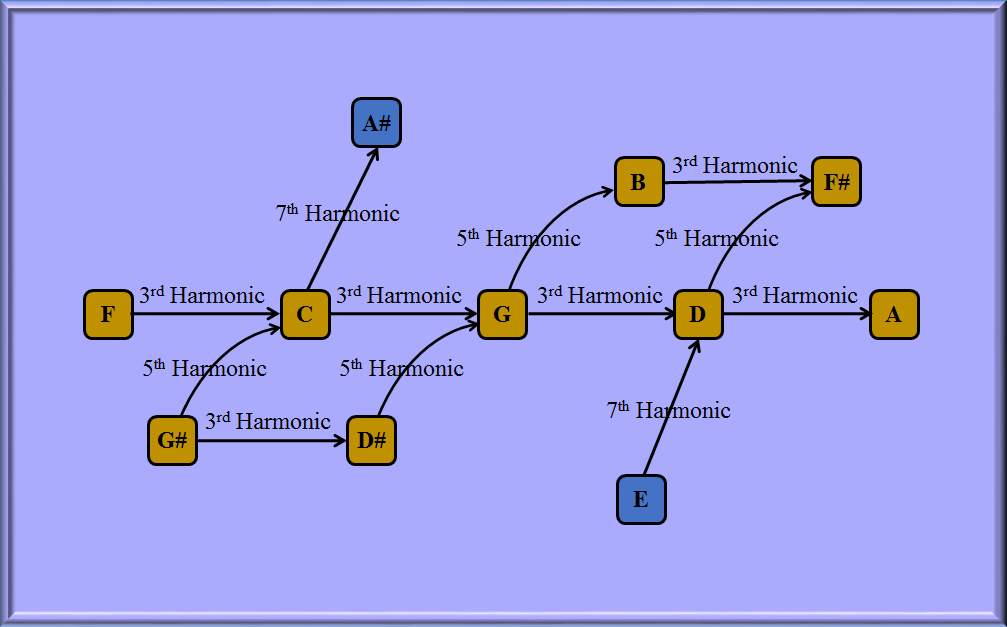
Luna Tuning is a Symmetrical Extended Just Tuning, using 3rd, 5th and 7th Harmonic ratios. The basic melody and accompaniment are in the Hexatonic scale G-A-B-C-D-E, but the excerpts from the Bach piece excurse from these six notes.
The numerical relationships of the notes are given in the table below.
| Luna Tuning | ||||
| Note | Integer Ratio | Decimal Ratio | Half-Step Interval | |
| G | 1 | 1.0000 | 1.0667 | |
| G# | 16/15 | 1.0667 | 1.0667 | |
| A | 9/8 | 1.1250 | 1.0547 | |
| A# | 7/6 | 1.1667 | 1.0370 | |
| B | 5/4 | 1.2500 | 1.0714 | |
| C | 4/3 | 1.3333 | 1.0667 | |
| C# | Sqrt(2) | 1.4142 | 1.0607 | |
| D | 3/2 | 1.5000 | 1.0607 | |
| D# | 8/5 | 1.6000 | 1.0667 | |
| E | 12/7 | 1.7143 | 1.0714 | |
| F | 16/9 | 1.7778 | 1.0370 | |
| F# | 15/8 | 1.8750 | 1.0547 | |
| G | 2 | 2.0000 | 1.0667 | |
The figure below depicts the layout of an imaginary single-string (a "G") Luna-Tuned fret board:
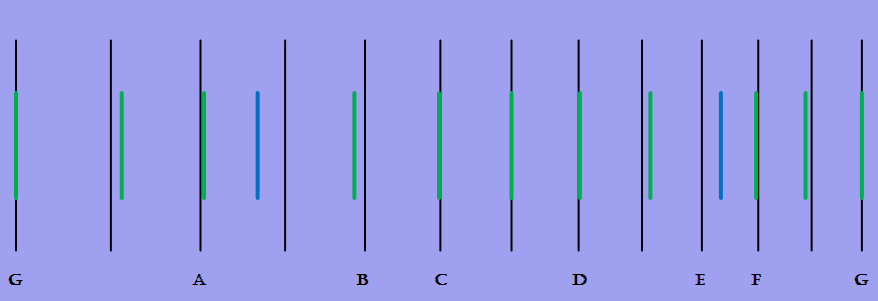
The colored bars indicate where the luna-tuned frets would be placed, with the black lines representing standard fret placement. Note that on a multi-stringed instrument the fret placement would be different for each string.
To see some Standard Just Intonation on a fretboard, visit Jim Snow's page
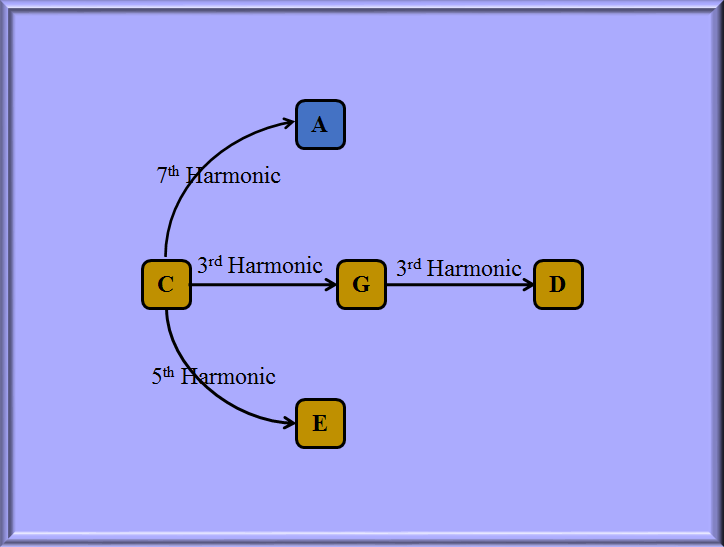
Take a Ride uses the Extended Just Pentatonic Tuning shown in the table below.
| Ride Tuning Relative to G | Ride Tuning Relative to C | |||
| Note | Ratio | Note | Ratio | |
| G | 1 | C | 1 | |
| A | 7/6 | D | 9/8 | |
| C | 4/3 | E | 5/4 | |
| D | 3/2 | G | 3/2 | |
| E | 5/3 | A | 7/4 | |
| G | 2 | C | 2 | |